Variable Acceleration
Variable Acceleration: Overview
This topic covers concepts such as Motion with Position Dependent Acceleration, Motion with Velocity Dependent Acceleration, Velocity Dependent Acceleration, Velocity Function in Velocity Dependent Acceleration, etc.
Important Questions on Variable Acceleration
The displacement of a particle varies with time as , where , , are positive constants. The velocity of the particle will
The displacement of a particle is represented by the following equation : where s is in metres and t is seconds. The acceleration of the particle at is
A Particle located at x = 0 at time t = 0, starts moving along the positive x-direction with a velocity that varies as . The displacement of the particle varies with time as –
The coordinate of a particle moving on x-axis is given by where is in and is time in seconds. Find the maximum distance the particle can move from the origin (in
A particle starts from point with zero initial velocity, moves along a straight line path with an acceleration given by where are constants and is distance from point The particle stops at point Find the maximum velocity of the particle when and
A particle moves in a straight line with a retardation proportional to its displacement. Its loss of kinetic energy for any displacement is proportional to,
A cart is moving horizontally along a straight line with constant speed . A projectile is to be fired from the moving cart in such a way that it will return to the cart after the cart has moved . At what speed (relative to the cart) must the projectile be fired (take )?
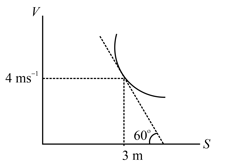
A particle is moving along a straight line whose velocity-displacement graph is as shown in the figure. What is the magnitude of acceleration when displacement is ?
Under the influence of a force of attraction towards the origin , a particle of mass moves. The force is given by expression . If the particle starts from rest at , find the speed it will attain to reach when it is at a distance from the origin.
The magnitude of displacement vector of a particle moving in a circle of radius with constant angular velocity ω as a function of time is
A particle starts from point A and moves along a straight line path with an acceleration given by a = p – qx where p, q are constants and x is distance from point A. The particle stops at point B. The maximum velocity of the particle is
The velocity of a particle at any instant is . The equation of trajectory of the particle is:
If the velocity of a particle is , where and are constants, then the distance travelled by it between and is:
The position (x) of a particle varies with time as , then acceleration of particle is
A point moves with uniform acceleration and its initial speed and final speed are and respectively then, the space average of velocity over the distance moved is. (in ) :-
The distance from the origin of a particle moving in plane varies with time as and the angle made by the radius vector with positive -axis is . Here, is in second, in metre and in radian. The speed of the particle at is
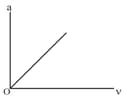
Acceleration velocity graph of a particle moving in a straight line is as shown in figure. The slope of velocity-displacement graph
A bee files a line from a point to another point in with a velocity of . The distance between and in metre is
Acceleration of a body for displacement equation, is
The acceleration of a particle moving in straight line is defined by the relation , where is acceleration in and is the position in meter. If velocity when x = 0, then the velocity of the particle when x = 4 meter is: